MEDICIÓN DEL RIESGO-LA DESVIACIÓN ESTÁNDAR

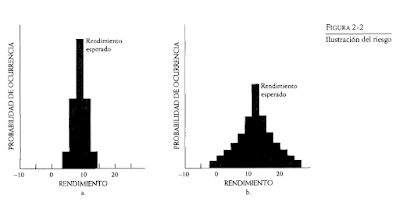
Hasta ahora hemos trabajado solamente con el rendimiento esperado al retener un valor. En un mundo de incertidumbre, quizás no se logre este rendimiento. Se puede pensar en el riesgo como la posibilidad de que el rendimiento real al retener un valor se desvíe del rendimiento esperado. Se dice que será mayor el riesgo del valor cuanto mayor sea la magnitud de la desviación y mayor la probabilidad de que ocurra. La figura 2-2 muestra las distribuciones de probabilidad del rendimiento posible para dos valores.

Puesto que el rendimiento real del valor B tiene una mayor probabilidad de desviarse de su rendimiento esperado que el del valor A, decimos que corre un mayor riesgo. Aunque el inversionista está preocupado principalmente por un riesgo de descenso, o la posibilidad de un rendimiento negativo, para facilidad de uso nuestra medición del riesgo toma en cuenta todas las divergencias del rendimiento real de lo que se esperaba.
Para ilustrar esta medición, supongamos que un inversionista creyera que el rendimiento posible a un año al invertir en acciones comunes específicas fuera el que se muestra en la tabla 2-7.

Se puede resumir esta distribución de probabilidades en términos de dos parámetros: el rendimiento esperado y la desviación estándar.

El rendimiento esperado es

Donde R. es el rendimiento de la eava posibilidad, Pi es la probabilidad de concurrencia de ese rendimiento, y n el número total de posibilidades. La desviación estándar es

Donde √ representa la raíz cuadrada. También se le puede expresar como [] 1/2. El cuadrado de la desviación estándar, a2, se conoce como la varianza de la distribución. Para ilustrar estas mediciones, consideremos nuevamente la distribución de rendimientos posibles que se muestran en la tabla 2-7. El rendimiento esperado es

La desviación estándar es