A continuación describimos los supuestos del modelo de Solow-Swan.
Primer Supuesto. Función de producción neoclásica.
Propiedades de la función de producción neoclásica.
i) Rendimientos constantes a escala. Es decir la función de producción es homogénea de grado uno.
Que la función de producción sea homogénea de grado uno significa que si el capital y el trabajo se multiplican por un número λ, entonces la producción total también se multiplica por λ.
ii) Rendimientos decrecientes del capital y del trabajo cuando estos se consideran por separado.
iii) Condiciones de Inada.
Segundo Supuesto. Suponemos una economía cerrada, lo que implica que las exportaciones e importaciones son nulas. Como la economía no comercia con el exterior en esta economía el producto interior bruto es igual al producto nacional bruto.
Tercer Supuesto. No hay gobierno, lo que implica que el gasto público es cero. Tampoco hay impuestos ni transferencias.
Al no haber impuesto (ni directos ni indirectos, y tampoco transferencias) el valor de la producción es igual a la renta.
Bajo los supuestos establecidos en este modelo la producción total se reparte entre consumo e inversión.
La renta de los agentes se dedica a consumir o a ahorrar:
de lo que se deduce que en la economía descrita en este modelo la inversión es igual al ahorro:
Cuarto supuesto. Se supone que los consumidores ahorran una proporción constante de la renta.
donde denota la propensión marginal al ahorro.
Bajo este supuesto el consumo de las familias es igual a (1-s)Yt.
Quinto Supuesto. Se supone que el stock de capital se deprecia a una tasa constante que denotamos por δ.
Sexto Supuesto. Se supone que el nivel de desarrollo tecnológico, que denotamos por A, se mantiene constante.
Séptimo Supuesto. La población crece a una tasa constante que denotamos por n.
En toda economía el stock de capital en t+1 es igual al stock de capital en t inversión bruta en capital fijo menos la depreciación:
denotando la variación del stock de capital por K (K=Kt+1-Kt) la inversión bruta se puede expresar como sigue:
Bajo los supuestos establecidos por el modelo de Solow-Swan la ecuación (2) puede expresarse como:
Despejando K de la ecuación (3) tenemos la ecuación que describe elcomportamiento dinámico del stock de capital:
Primer Supuesto. Función de producción neoclásica.
Propiedades de la función de producción neoclásica.
i) Rendimientos constantes a escala. Es decir la función de producción es homogénea de grado uno.
Que la función de producción sea homogénea de grado uno significa que si el capital y el trabajo se multiplican por un número λ, entonces la producción total también se multiplica por λ.
ii) Rendimientos decrecientes del capital y del trabajo cuando estos se consideran por separado.
iii) Condiciones de Inada.
Segundo Supuesto. Suponemos una economía cerrada, lo que implica que las exportaciones e importaciones son nulas. Como la economía no comercia con el exterior en esta economía el producto interior bruto es igual al producto nacional bruto.
Tercer Supuesto. No hay gobierno, lo que implica que el gasto público es cero. Tampoco hay impuestos ni transferencias.
Al no haber impuesto (ni directos ni indirectos, y tampoco transferencias) el valor de la producción es igual a la renta.
Bajo los supuestos establecidos en este modelo la producción total se reparte entre consumo e inversión.
La renta de los agentes se dedica a consumir o a ahorrar:
de lo que se deduce que en la economía descrita en este modelo la inversión es igual al ahorro:
Cuarto supuesto. Se supone que los consumidores ahorran una proporción constante de la renta.
donde denota la propensión marginal al ahorro.
Bajo este supuesto el consumo de las familias es igual a (1-s)Yt.
Quinto Supuesto. Se supone que el stock de capital se deprecia a una tasa constante que denotamos por δ.
Sexto Supuesto. Se supone que el nivel de desarrollo tecnológico, que denotamos por A, se mantiene constante.
Séptimo Supuesto. La población crece a una tasa constante que denotamos por n.
En toda economía el stock de capital en t+1 es igual al stock de capital en t inversión bruta en capital fijo menos la depreciación:
denotando la variación del stock de capital por K (K=Kt+1-Kt) la inversión bruta se puede expresar como sigue:
Bajo los supuestos establecidos por el modelo de Solow-Swan la ecuación (2) puede expresarse como:
Despejando K de la ecuación (3) tenemos la ecuación que describe elcomportamiento dinámico del stock de capital:









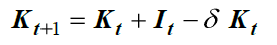








No hay comentarios:
Publicar un comentario